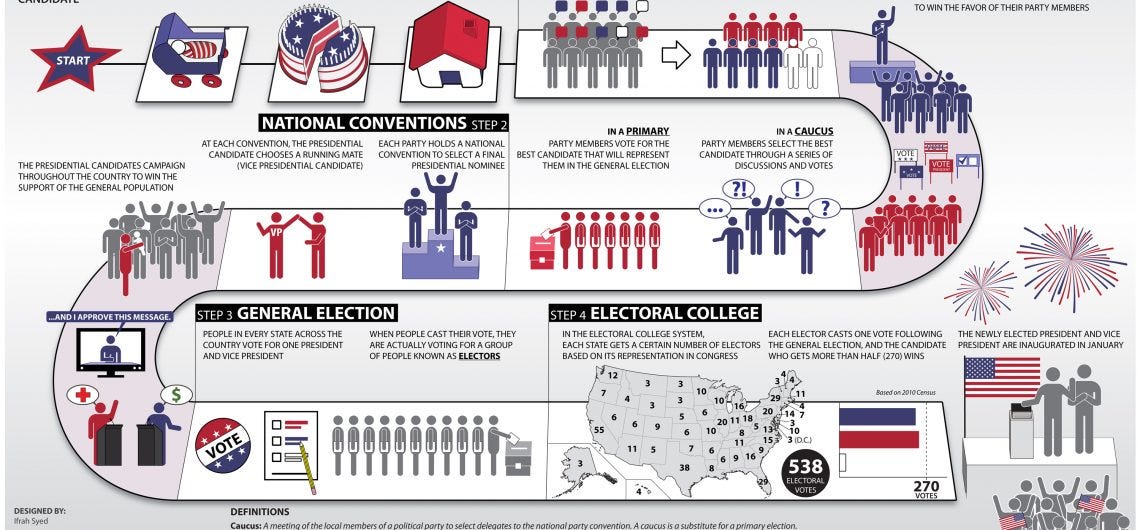
I moved to the US and experienced the presidential elections first-hand. There was a lot of emotions, and like every elections, discussions about whether the electoral system is fair, and what drawbacks it has. I started overthinking
What is the most optimal electoral system?
Why are two competing political parties always so evenly matched in the number of votes?
How can people strategize in elections? Why isn’t it just about who our favorite is?
And found that there are many very weird things about voting. Here are 5 different “paradoxes” of voting systems.
Paradox 1: Different types of voting lead to different results
Paradox 2: There’s no ideal voting system
Paradox 3: Getting more votes can lead to a candidate’s loss, and fewer votes to their win
Paradox 4: Voters can kill one option by voting for a different version of it
Paradox 5: Candidates will adapt to attract the “average person”
Recap: Types of voting
Before we get into the paradoxes, I want to summarize some common types of voting. There are many ways to vote for something (and I don’t necessarily mean voting in politics).
Majority voting: Winner needs >50% of votes. Favors candidates with broad appeal.
Plurality voting: Highest vote-getter wins, even without majority. Favors candidates with strong base support.
Proportional voting: Seats allocated based on vote share. Favors diverse representation and minority voices.
Borda count: Rank all candidates, points assigned by rank. Favors consensus candidates with broad second-choice support.
(Instant) runoff voting: Eliminate lowest-ranked candidate each round until majority winner. Favors candidates with strong core support plus acceptability to others.
Approval voting: Vote for multiple candidates, most approvals wins. Favors moderate, broadly acceptable candidates.
Range voting: Rate each candidate (e.g., 0-5), highest average wins. Favors candidates viewed positively by many voters, even if not their top choice.
Paradox 1: Different types of voting lead to different results
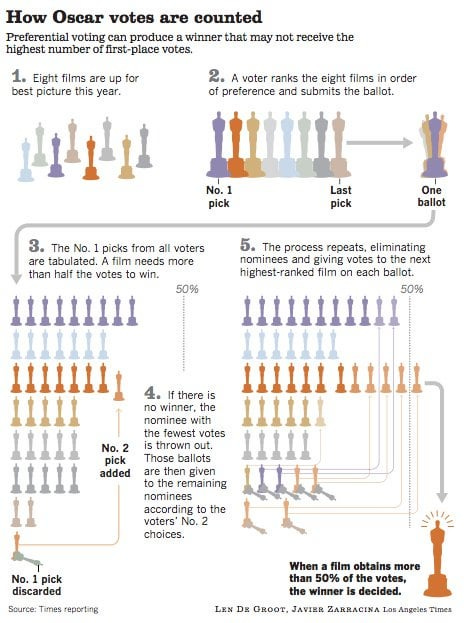
2016 elections case study showed that different voting methods led to different results. This is a nice demonstration of how “unproblematic” candidates like Sanders can win in range voting (he probably appeals to a lot of people to SOME extent and a few people have problems with him) while others can win in IRV or Plurality (Clinton or Trump might have very strong supporters but also strong haters).
Paradox 2: There’s no ideal voting system
Arrow's Impossibility Theorem states that no voting system can simultaneously satisfy all of the following fair criteria
Non-dictatorship (there’s no individual or small group that decides about the results)
Pareto efficiency (if each voter prefers candidate A over B, candidate A should also be preferred when you consolidate the votes)
Independence of irrelevant alternatives (if candidate A wins over B, they should win regardless of what other options are there. It shouldn’t influence this preference.)
You can read this theorem in formal mathematical notation on Wikipedia, and even see a proof of it.
The important takeaway of Arrow’s Impossibility Theorem is also that there is no good way to consolidate individual preferences into group preferences. But what if we come with a system that satisfies all three criteria, and we try to consolidate the preferences into group preferences? Condorcet’s paradox shows one such case.
Example: Condorcet’s paradox
This is an example where all three conditions of the Arrows Impossibility Theorem are satisfied, but it leads to a nonsense social welfare function. Such a function then contradicts the rules of logic.
Imagine that people vote for candidates A, B, and C like this:
When you consolidate the results, you get to cyclical preferences, which contradicts basic logic. You can’t choose a candidate that would beat all other candidates in 1:1 competition.
A simpler version is this:
We shouldn’t be too worried about this paradox. Even though mathematically, this paradox is proven to occur in ~10% of cases, in reality, it was measured to occur in ~1%. That’s because the options aren’t usually independent. E.g., if A, and B are very similar options, not many people will vote A > C > B or B > C > A, because they will either like both A, and B, or neither.
One example of Condorcet’s paradox is Brexit.
Paradox 3: Getting more votes can lead to a candidate’s loss, and fewer votes to their win
The monotonicity paradox happens when a candidate who gains more votes in an election ends up losing as a result, or a candidate who loses votes ends up winning.
I drafted an example, using the Instant Runoff Voting (IRV) system - the one that eliminates the lowest-ranked candidate each round until you get a majority winner.
In the first case, candidate B wins. However, if B gets more votes, the elimination order will be altered. In the second case, candidate D is eliminated instead of E, and D's votes are redistributed. Because you eliminate candidates in different orders, B doesn’t win in the end.
I am not sure if my example is mathematically correct, but it helps to get the idea.
Paradox 4: Voters can kill one option by voting for different version of it
The killer amendment is a situation in legislative voting where introducing and passing an amendment strategically kills the original proposal.
In this example, Democrats and Republicans were deciding between approving vs not approving federal aid for school construction.
The three options hence looked like this:
O: Federal aid for school construction (original proposal).
A: Federal aid with an amendment prohibiting funds for segregated public schools.
N: Status quo (no federal aid).
The process can be summarized in the following voting structure:
Round 1: Vote on whether to include the amendment (Option A) or not (Option O).
Round 2: If Option A wins, voters then decide between the amended bill (A) or the status quo (N).
In this example, the Republicans took advantage of the voting procedure to strategically “kill” the original bill. They knew that many Democrats would prefer to vote against the bill if it included an amendment prohibiting funds for segregated schools. By choosing the version with this amendment (Option A) in the first round, Republicans ensured that the amendment would pass, which made the bill less likely to be approved by Democrats. This tactic effectively killed the original proposal, as Democrats would likely oppose it with the amendment attached.
There are many more real-life examples like this:
Paradox 5: Candidates will adapt to attract the “average person”
Have you ever wondered why the two leading political parties in the US also end up very close to each other in the results?
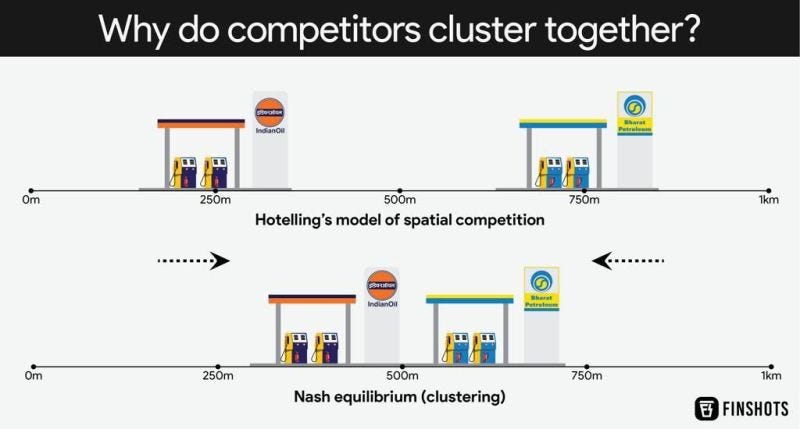
One way to explain it is with *checks notes* ice cream stands. See this:
This most optimal state for both ice cream stands on the beach is right in the middle of the beach. In general, such an ideal state is called Nash Equilibrium. It is when no player can improve by changing their strategy, given what others are doing.
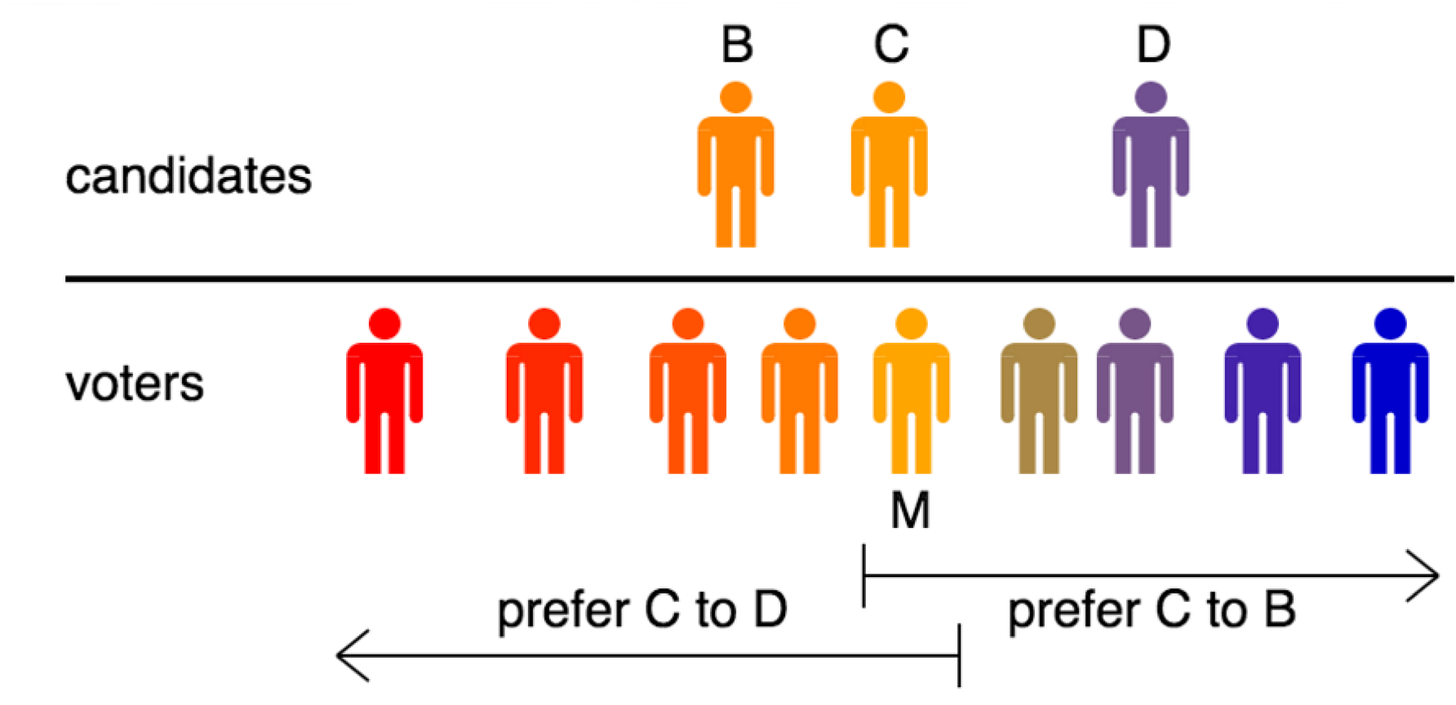
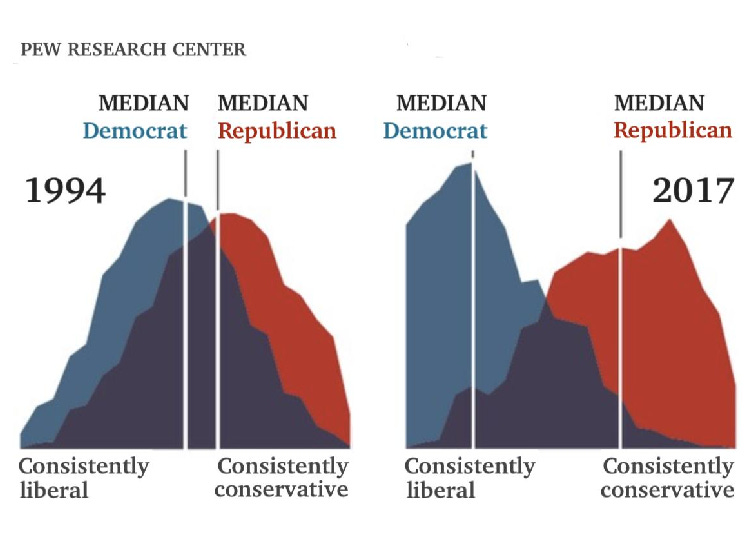
There might be similar intuition behind two opposite political parties converging to the “middle” of people’s preferences. The Median Voter Theorem is a principle in political science that suggests that in a majority-rule voting system, the candidate who positions themselves closest to the preferences of the median voter is most likely to win.
In traditional two-party systems, the Median Voter Theorem suggests parties gravitate toward centrist positions to capture the median voter.
However, this theory oversimplifies modern political reality in two ways: First, political positions exist in a complex, multi-dimensional space rather than on a simple left-right spectrum.
Second, recent evidence, as shown in the Pew Research graph, reveals increasing ideological polarization between parties rather than convergence. This divergence from the theorem's predictions raises questions about whether factors beyond median voter preferences now drive party positioning. I think this is an interesting topic for discussion.