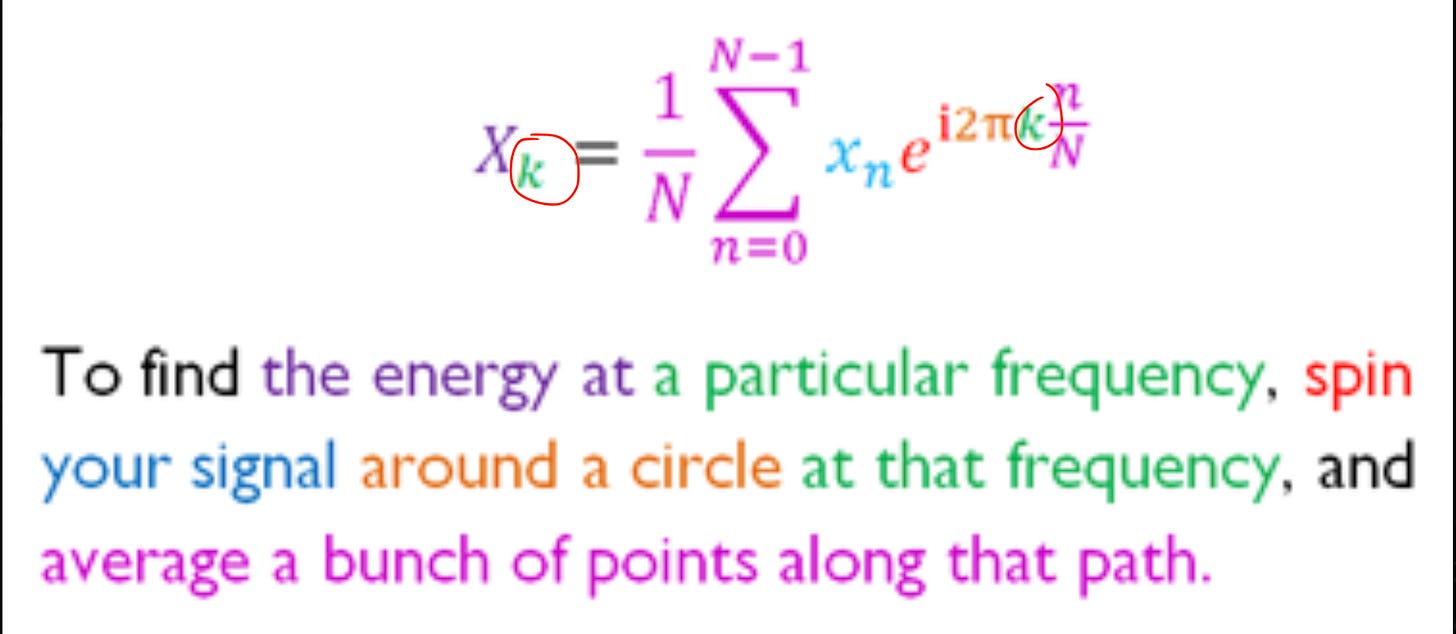Simplest Explanation of Fourier Transform?
A few notes on the viral "Fourier Transform explained in one sentence"
I’ve just seen this post on X (Twitter).
This image presents the Discrete Fourier Transform formula along with a colorful explanation of its physical interpretation.
I am not even sure if the image helped me understand Fourier transforms in case I didn’t understand them already. Share your opinion, please.
I think the eternal problem with explaining technical content to a non-technical audience is too many new concepts at once. Even if explained super-simply, using visualizations, colors, metaphors, people still say that it’s too much.
Explanation
That’s why I decided to break it down to even more basic facts. Here is some more explanation of the image.
Let’s look at the colorful sentence step-by-step.
1. “To find…”
Why we want to find the energy? The math behind Fourier transforms has found many many use cases. It is applied in Physics, Biology, Robotics, Finance, and even the music industry. Let’s say we are finding specific type of energy, which can have different meaning across different fields, but is really important.
2. “To find the energy”
Examples of energy can be sound waves. When you hear music, different notes have different frequencies, and the "energy" at each frequency tells you how loud each note is.
3. “To find the energy at a particular frequency”
This means we FIX a condition (a given frequency) and find the energy just for that one case. In math, we denote constants by k and usually label the thing we look for (denoted by X) by that. Notice that the k appears on the right side of the equation too.
4. “To find the energy at a particular frequency, spin your signal”
This is the part where people on Twitter started being angry, and I am not surprised.
The spinning is represented by the e^i term. Here we have to use some math to see how the hell this spins the signal or whatever. First, “to spin” intuitively tell you that we want to do a movement around a circle, right?
How do we do this? We multiply each signal point (blue x) with a “magic formula” and get a point on a circle. We do this for many different signals (different x_n, because the n just starts at 0 and ends at N - 1), so we essentially achieve some sense of movement (spinning) around a circle.
5. “To find the energy at a particular frequency, spin your signal around a circle”
But how the hell this:
Makes the x_n spin around a circle?
Now we need to accept some Mathematical facts and move on. There is a famous formula called the “Euler formula”:
In our case, the θ is basically the 2πk(n/N):
It says that if we take θ and use it as an exponent with the e (the left part of the Euler formula), it gives us a point on a circle (the right part). You don’t have to care now why the formula looks exactly like this.
Geometrically, θ is an angle.
6. “To find the energy at a particular frequency, spin your signal around a circle”
So by the “spinning around a circle”, we are saying that we just paste many different points into the formula, and show them as a point on a circle, that is, we are rotating with the points around a circular shape. The stuff I circled in red is just a “mechanism” that takes each point we give it, and returns a position on the circle.
Here is a comment from AI on why exactly the “mechanism” of plotting points on a circle looks like that:
7. “To find the energy at a particular frequency, spin your signal around a circle at THAT frequency”
This is just saying “By the way, we said we want to do this for some fixed constant frequency (denoted by k), don’t forget to stick to it, and paste that particular frequency to the formula.
8. “To find the energy at a particular frequency, spin your signal around a circle at THAT frequency, and average a bunch of points along that path.”
This is also Math. Yes, there are a lot of n’s and N’s. That’s mathematicians’ way of saying that we apply this weird “mechanism” in many many instances. I loosely use “mechanism” instead of “function”. Just a formula where you paste a value and get something in return.
The big sum just says we make some kind of average. It just corresponds to the summation and division by N in the formula, which effectively leads to calculating the average.
I would conclude that you take bunch of small x (signals) and somehow get the big X (energy) through this “mechanism”. As I said, Fourier transforms are used across different fields, so just look for particular examples.
The signal can be something like a digital sound recording. I found an article about the formula where signal and frequency are explained like this:
And I think that’s really nice.
Disclaimers
There are more types of Fourier Transform btw, but the intuition is similar.
This post was written in one hour by the fireside, and it’s my lowest-effort post ever. I am really proud of that because my goal is to write more often about all the interesting things in this world, but I struggle to keep it casual, so in the end I don’t manage to write everything I want. This is the first small step!