Topological Quantum Computers Explained
Topological quantum computers explained, how topology helps there, and what it is
About the Quantum Computing Series
Understanding quantum computing requires understanding multiple disciplines. That’s why it’s one of my favorite topics to write about, but also why I prefer to look at it from a mathematical point of view, which I’m most comfortable with. In this chapter, I explain what is meant by topological quantum computers and what magic topology does for reducing the errors of qubits.
Enjoy the reading & see the complete Quantum Computing Series listed at the conclusion of this post.
Intro
Topological quantum computers are the “next big thing” in quantum computing. But what exactly does “topological” mean, and why does it hold such a great potential?
Typically, when someone tries to explain topology to you, they wave their hands and tell you something like
“Topology deals with properties that “depend only on shape”
or
“In topology, two objects are considered equivalent if they can be continuously deformed into one another”.
Plus, I bet that there is a donut involved in the explanation (being deformed into a mug☕️ if you are lucky.)

I will attempt to explain topology and its importance, using topological quantum computing as an illustrative example.
Prerequisites
Here is a quick intro to standard quantum computers.
1. Traditional computers
Pro tip: If you are afraid that you do not understand quantum computers, ask yourself how well you understand even classical computers.
Computers use bits for storing information. Bits are abstract (!) units of information that can hold a value of 0, or 1. It’s just a logical state.
Physically, there are transistors — something that allows computers to process bits. A transistor is a small semiconductor device that I imagine as a switch. A transistor can either allow current to pass through or block it, which corresponds to the binary states 1 and 0.
The important take for you is that we have something physical in the computer that allows us to represent two different values (0, or 1). Computers contain hundreds of billions of transistors.
But what if we want to represent more than two states?
2. Quantum computers
These store information in qubits instead of bits.
Qubits, unlike classical bits, have a more direct physical representation because they are quantum objects. Qubits are typically electrons or photons, in general just very small particles.
Note that for both bits and qubits, there is not a unique way to represent bits and qubits, but a variety of approaches.
For example in photonic qubits, the polarization of a photon (the direction in which the electric field oscillates) is used to represent the qubit’s states. I don’t like the saying that it “can exist in more states at once”, but I would say qubit can get into any linear combination of 0 and 1 (that is, any state between these), with a certain probability of each of these two states.
🧠 If you want to understand the principles, here are my favorite resources on quantum:
DOE Explains…Quantum Mechanics by Energy.gov
Explainer: What is a quantum computer? by MIT Technology Review
What is quantum computing? by IBM.
The problem of quantum computers
Qubits allow quantum computers to perform many operations at once, making them faster and more powerful.

However, many current implementations of qubits, such as trapped ions and superconductors, are highly susceptible to noise and decoherence. It’s because the particles (qubits) travel through an environment (medium), causing collisions that lead to noise, and hence errors.

Topological quantum computing
Quantum computers solve the problem of noise thanks to their topological nature.
Bits occur in classical computers and are represented by two-state devices.
Qubits occur in quantum computers and are represented by particles.
In topological quantum computers, qubits are represented by something called quasiparticles - one last prerequisite we need to understand here.
Quasiparticles
A quasiparticle is a collection of quantum characteristics among particles operating in their own, particle-like way. Quasiparticles arise from the collective behavior of many underlying particles. Unlike regular particles, they don’t exist independently; they are just excitations within a material and they behave like particles.
I love this illustration of quasiparticles, which originates from the physicist Richard Mattuck.
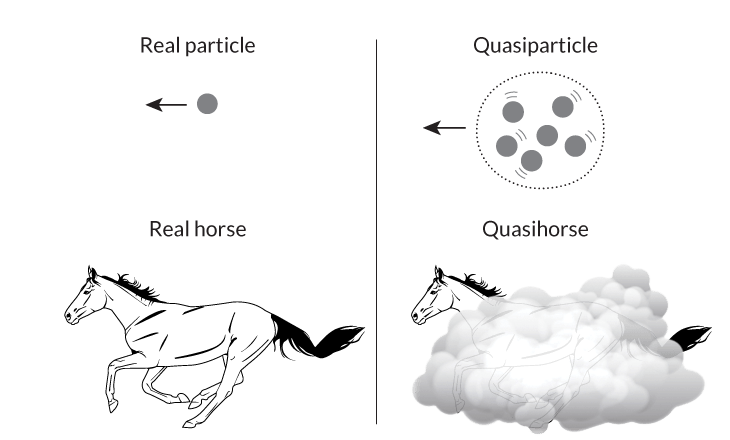
In topological quantum computers, the noise can then be modeled by quasiparticles traveling through a vacuum with a different mass.
🧠 Here are good additional resources on quasiparticles:
Quasiparticles help physicists make sense of the world by ScienceNews
How Are Quasiparticles Different From Particles? by PBS Space Time
Microsoft, the only (as far as I know!) company making progress in topological quantum computing today, uses quasiparticles called Majorana zero modes.
How topology helps
The solution to the noise problem is all about how the information is stored.
Remember, in classical computers, the information is stored in bits.
In a topological quantum computer, information is NOT encoded in the quasiparticles themselves though. Instead, it is encoded in the manner in which they interact and how they are braided together.

A crucial property of the braids of quasiparticles is that local perturbations (noise) will not impact the state of the system unless these perturbations are large enough to create new braids.
This is super-important and in fact, it is an informal way of saying that the braids have a “topological property”, which is a strong mathematical claim.
Topological property
The way the quasiparticles are braided is a topological property. This is a formal mathematical term (also often called a topological invariant).
We say something has a topological property when such property stays the same under “continuous deformations” (officially called “homeomorphism”).
This is actually an important concept that I think is the core to understanding why topology is cool to study (wink wink).
Some examples of topological properties (in general, not related to quantum computing):
1. Relations of nodes in a graph
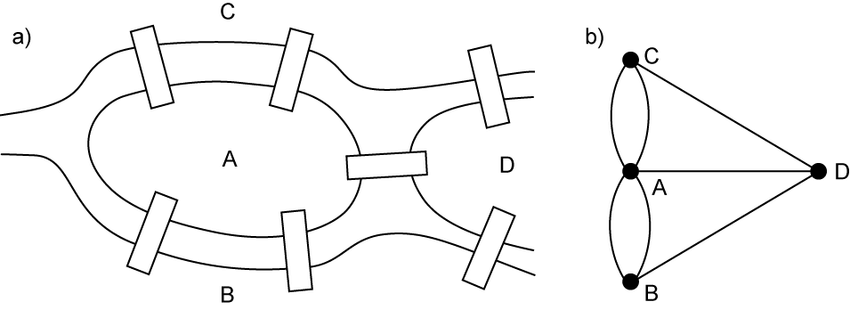
In graphs, it only matters to us whether the two vertices are or aren’t connected. We can stretch the graph, and deform it, but if we don’t cut it, the meaning of the graph is the same.
Topology actually started with the famous Königsberg bridge problem solved by Euler. The problem was wondering whether a citizen could take a walk through the town in such a way that each bridge would be crossed exactly once.
This problem can be generalized and solved by looking at the city with bridges as a graph. It can be deformed into the graph on the right because the property of pieces of land being connected by a bridge is invariant under such continuous deformations.
Two vertices in the graph are connected by an edge if an only if two corresponding pieces of land on the left picture are connected by a bridge.
Deforming the city into a graph didn’t change the relationships we study here.
2. Relationship between vertices, edges, and faces of a graph
Euler (the same mathematician who solved the Seven Bridges problem) showed that for surfaces with the same number of holes, V — E + F = the same number. (V = vertices, E = edges, F = faces).
For example for surfaces similar to the polyhedra below, V — E + F = 2 every time.
Again, the relationship between V, E, and F is a topological property. It isn’t changed if the given surface gets slightly deformed, made bigger or smaller, etc.
3. Number of holes in a surface
This one is the classic, and it is why in that one infamous meme, a donut and a cup are claimed to be the same thing. Topologically, they are the same, because they are shapes that have the same number of holes.
If you had a plasticine donut, you could deform it to make a cup, without cutting and disconnecting anything. Mathematically we say the spaces with the same number of holes have the same genus. The genus is a topological property (invariant) too.
There are more concepts like this in topology, and indeed it needs a formal mathematical language to define them. However, I hope you get that the idea behind topology is caring only about certain properties of spaces. In topological spaces, we don’t care about distances or sizes, we just care about shapes and relations of certain points.
Back to quantum computing…
We have learned that quasiparticles used in topological quantum computers form braids that are not changed by noise. The braids are topologically invariant.
If we deform a braid, it remains a braid and cannot un-braid.
Here I tried to sketch that if you “slightly” move the purple braid, it is still braided together in the same way. You would have to cut some of the braids or make very drastic movements to change the way of braiding.
One more thing I consider useful when visualizing how it works is being aware that the quasiparticles occur in a two-dimensional space while the braid-like patterns occur in a three-dimensional space (two spatial dimensions plus time).
The braids basically act as logic gates, basic building blocks of (quantum) computing. And, as the last reading resource, I recommend simply checking out the Wikipedia page on Topological quantum computers.
Summary
In this post, I was secretly trying to manipulate you into liking topology, but also now we have the basics for (topological) quantum computing.
There are quantum computers, which are faster and more powerful than normal computers. They use qubits instead of bits. Qubits are represented by particles.
However, quantum computers are not that precise due to noise affecting the particles.
Researchers came up with a potential solution: Topological quantum computers. Instead of particles, they use quasiparticles which are collections of particles and they are immune to noise.
The reason quasiparticles are immune to noise is that they form “braids” which have topological properties. That is, a property that doesn’t change under deformations, that is, isn’t affected by noise.
Read more of the Quantum Computing Series:
Chapter 1: Microsoft and Google's Quantum Launches
Chapter 2: Building a quantum computer
Chapter 3: Types of quantum computers
Chapter 4: Quantum computers market
Chapter 5: Topological Quantum Computers Explained
Resources to start with quantum computing
What Quantum Computing Isn't by Scott Aaronson
Learn the Algorithms Behind Quantum Computing by Beau Carnes
Landscape of Quantum Computing in 2024 by Samuel Jaques
Quantum Computing on Wikipedia









Excellent article. Great explanations and to the point. With a good collection of reference resources.